Geometric Mechanics, Control, and Learning
Many interesting dynamic systems in science and engineering evolve on a nonlinear, or curved, space that cannot be globally identified with a linear vector space. Such nonlinear spaces are referred to as manifolds, and they appear in various mechanical systems such as a simple pendulum, rotational attitude dynamics of a rigid body, or complex multibody systems.
Our research is focused on constructing computational geometric methods for dynamics and control of mechanical systems evolving on a nonlinear manifold. The central idea is constructing nonlinear control systems directly on nonlinear manifolds, and verifying their performances numerically by using geometric numerical integrators that preserve the underlying geometric properties of a dynamic system. All of these are expressed in a coordinate-free form to avoid any singularities, ambiguities, and complexities inherent to local parameterizations. These allow us to study non-local, large, and aggressive motions of complex dynamic systems globally in an accurate and efficient fashion over a long period.
*Featured Topic: Matrix Fisher--Gaussian Distribution on SO(3) x Re^n
What should be a Gaussian distribution for attitudes?Gaussian distributions, that are commonly known as the bell curves, are the most celebrated probability distribution in science and engineering. According to the central limit theorem, the sum of a large number of independent random variables tends toward a normal distribution, and the majority of the estimation schemes, such as the Kalman filter, are derived analytically in an explicit form when the relevant random variables are normally distributed.
However, attitude evolves on a compact, Lie group, referred to as the special orthogonal group. Consequently, Gaussian distributions defined in the Euclidean space cannot be adopted to attitudes, unless they are adopted to local coordinates heuristically while causing a lot of troubles, such as singularities and complexities.
To address these, we propose a probability density for attitude uncertainties, referred to as matrix Fisher distribution that is globally formulated on the special orthogonal group. In fact, this resembles the Gaussian distribution for three-dimensional vectors: the resulting marginal distribution of each body-fixed axis is ellipsoidal on the unit sphere; nine parameters specify the mean attitude, the principal axes of rotations, and the degree of concentration along the principal axis. This is similar to the Gaussian distribution that is defined by the mean, the principal axes, and the lengths of the semimajor axes of Gaussian ellipsoids. However, in contrast, the matrix Fisher distribution is globally formulated on the special orthogonal group without need for local coordinates.
Utilizing these, Bayesian attitude estimators and unscented attitude estimators are constructed. It has been illustrates that these are particularly useful for challenging cases that the initial attitude is completely unknown, or single direction measurements are available only. See the following documents and code for details.
- W. Wang, T. Lee, "Matrix Fisher--Gaussian distribution on SO(3)xRe^n for Bayesian attitude estimation," IEEE Transactions on Automatic Control, 2020, submitted.
- W. Wang, K. Gamagedara, T. Lee, "On the observability of attitude with sing direction measurements" IEEE Transactions on Automatic Control, 2020, submitted.
- W. Wang, T. Lee, "Higher-order central moments of matrix Fisher distribution on SO(3)," Statistics and Probability Letters, 2020, submitted.
- W. Wang, T. Lee, "Matrix Fisher--Gaussian distribution on SO(3)xRe^n for attitude estimation with a gyro bias," Proceedings of the American Control Conference, 7 2020.
- T. Lee, "Continuous-time attitude smoothing with matrix Fisher distribution on SO(3)," Proceedings of American Control Conference, 2021, submitted.
- T. Lee, "Bayesian Attitude Estimation with the Matrix Fisher Distribution on SO(3)," IEEE Transactions on Automatic Control 2018, doi: 10.1109/TAC.2018.2797162
- T. Lee, "Bayesian Attitude Estimation with the Matrix Fisher Distribution on SO(3)," arxiv:1710.03746 2018
- https://github.com/fdcl-gwu/Matrix-Fisher-Distribution
- T. Lee, "Spacecraft attitude estimation with a single magnetometer using matrix Fisher distributions on SO(3)," Proceedings of the AIAA Guidance, Navigation and Control Conference, January 2019, {AIAA} 2019-1173.
- T. Lee, "Bayesian attitude estimation with approximate matrix Fisher distributions on SO(3)," Proceedings of IEEE Conference on Decision and Control, pp. 5319--5325, December 2018.
Geometric Controls on a Manifold
Most of the existing controllers for multibody systems are based on simplified dynamics models, and they often exhibit singularities when representing complex rotational maneuvers, thereby fundamentally restricting their ability to follow nontrivial trajectories. By explicitly utilizing geometric properties on a nonlinear manifold in Lyapunov stability analysis, we can construct an intrinsic form of control systems for the complete dynamics of multibody systems, while guaranteeing almost global asymptotic stability.More explicitly, the following topics have been studied:
- Geometric attitude controls on SO(3)
- Geometric control for quadrotor unmanned aerial vehicles
- Autonomous aerial payload transportation
- Spacecraft attitude controls
- Geometric attitude observer
Video: Geometric controls of a quadrotor UAV and cooperative payload transportation; control of flapping wing UAV
Video: Flight experiment for payload transpportation; Control of a flapping-wing UAV
Computational Geometric Optimal Control
Computational geometric optimal control approach is to find an optimal control for a dynamic system represented by discrete mechanical systems. This is in contrast to the conventional approach where a discretization appears in the last stage when solving an optimality condition numerically.This method has substantial computational advantages. Numerical solutions obtained by discrete mechanics are more faithful to general non-geometric integrators, and consequently more accurate solutions of optimal control problems are obtained. We also find optimal trajectories efficiently as this is free of artificial numerical dissipation introduced by conventional numerical integration schemes.
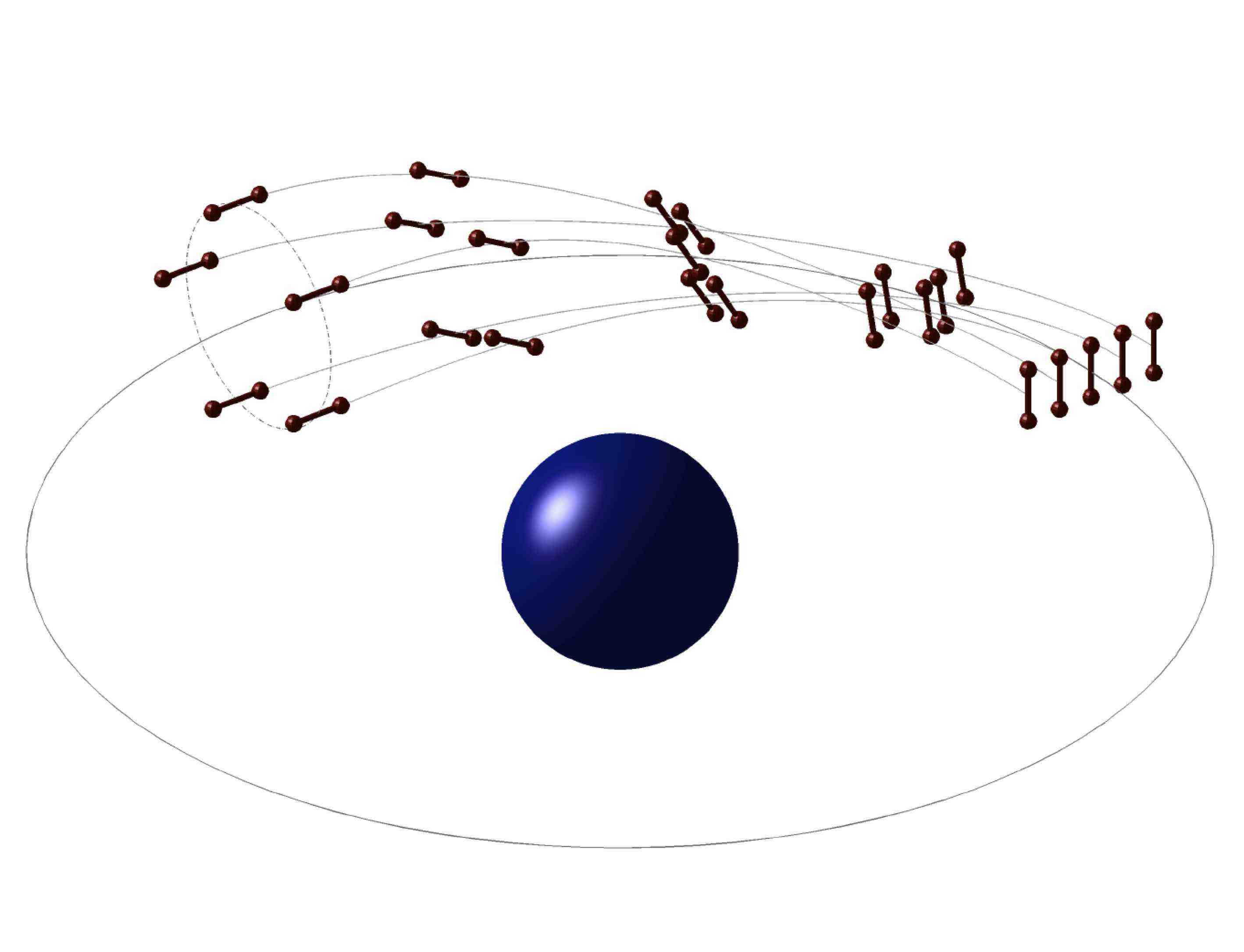
Optimal combinatorial formation reconfiguration of multiple spacecraft
Optimal control of articulated rigid bodies: snapshots of a 180 degrees rotation, achieved by using an internal control torque on a joint

Optimal control of connected rigid bodies in a perfect fluid: snapshots of forward swimming
Figure: Applications of geometric optimal control
Computational Geometric Mechanics
Geometric numerical integration deals with numerical integration methods that preserve geometric properties of a dynamic system, such as invariants, symmetries, reversibility, or the structure of the configuration manifold. The geometric structure of a dynamic system determines its qualitative dynamical behavior, however, general purpose numerical integrators fail to provide reasonable computational results. For example, numerical simulations based on the conventional implicit Euler method predict that the outer solar system collapses over a time period of several hundred years, but an integration over a hundred million years does not deteriorate with geometric integrators.We developed geometric numerical integrators, referred to as Lie group variational integrators for mechanical systems evolving on a Lie group, with applications to complex multibody systems. They are developed from the perspective that a geometric numerical integrator for a Lagrangian or Hamiltonian system is a discrete-time Lagrangian or Hamiltonian mechanical system. Therefore, their numerical solutions are consistent with continuous time dynamic characteristics: they are symplectic and momentum preserving, and they exhibit good energy behavior over a long time period. They also preserve the Lie group structures as the update algorithm is based on the corresponding group operation. A recent benchmark studies show that they have substantial advantages in computational accuracy and efficiency: when compared to other geometric integrators, the speedup factor varies from 16 times to 98 times.
Due to these computation advantages, Lie group variational integrators have been applied to various multibody systems. Most importantly, it has been used to study the dynamics of the binary near-Earth asteroid 66391 (1999 KW4) at the Jet Propulsion Laboratory, NASA. Other examples include spacecraft formation flight, rigid bodies connected by ball joints, articulated rigid bodies in a perfect fluid, and tethered spacecraft with a reeling mechanism.

Near-Earth binary asteroid 66391, collaboration with JPL NASA
Bending dynamics of a slender rod
Tethered spacecraft on a circular orbit
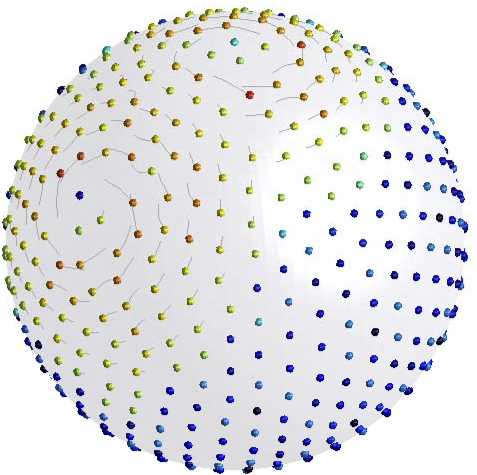
Molecular dynamics
Figure: Applications of Lie group variational integrators
Computational Geometric Uncertainty Propagation and Estimation
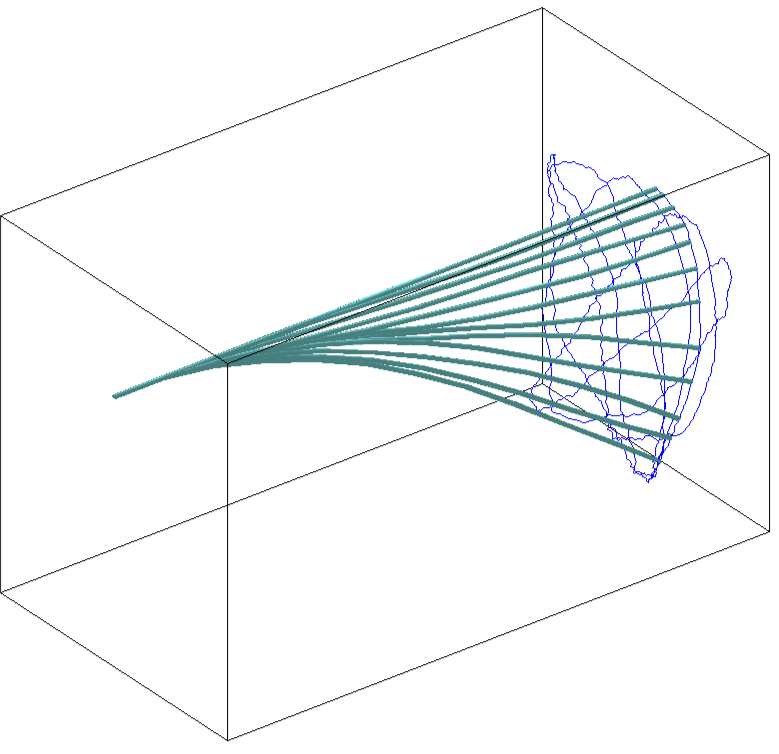
This is to develop computational geometric methods to propagate uncertainties through nonlinear Hamiltonian flows with stochastic excitations that evolve on nonlinear Lie group configuration spaces. The main objective is to derive computational methods that preserve the underlying stochastic and geometric properties of a Hamiltonian system to obtain long-term structural stability in the numerical uncertainty propagation. By incorporating mesh-free computational techniques that are globally valid on a Lie group, we obtained numerical algorithms that are well suited to propagating uncertainties along nontrivial trajectories of complex Hamiltonian systems over a long-time period. These represent significant advances over current computational methods that are restricted to moderate trajectories, simple dynamic properties, and short propagation times.We also developed attitude estimation algorithm directly on the special orthogonal group to avoid complexities, singularities, and ambiguities that appear in other attitude representation such as quaternions and Euler angles.
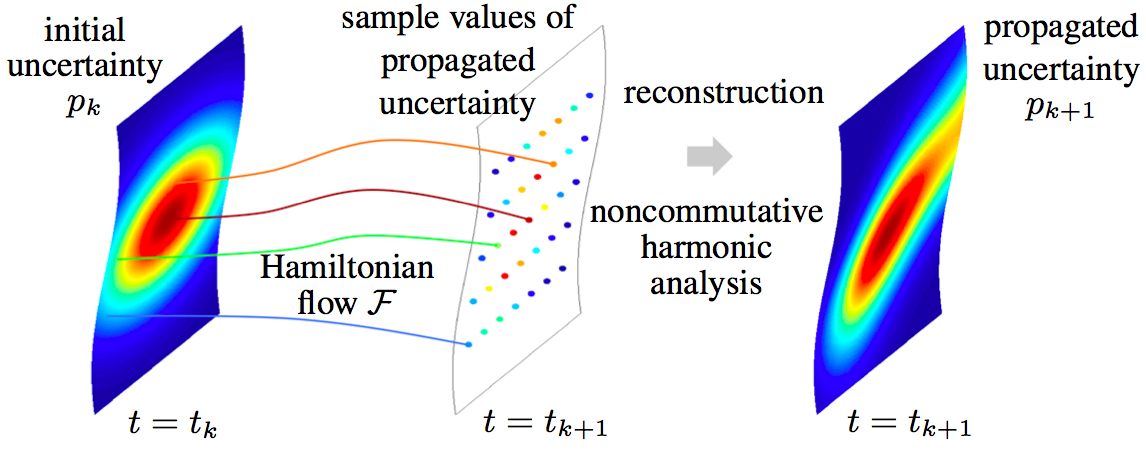
(Advection): the initial uncertainty (left) is propagated along Hamiltonian flows to obtain the sample values of the probability density (center); the propagated uncertainty (right) is reconstructed by using noncommutative harmonic analysis. (Diffusion): Liouville's equation representing the diffusion effects are converted into an ordinary differential equation, which is integrated numerically. (Splitting) the advection approach and the diffusion approach is combined by a splitting technique.
Figure: computational uncertainty propagation algorithm
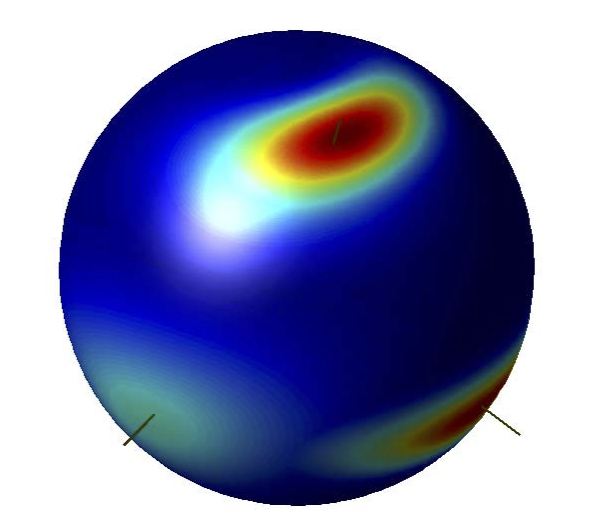
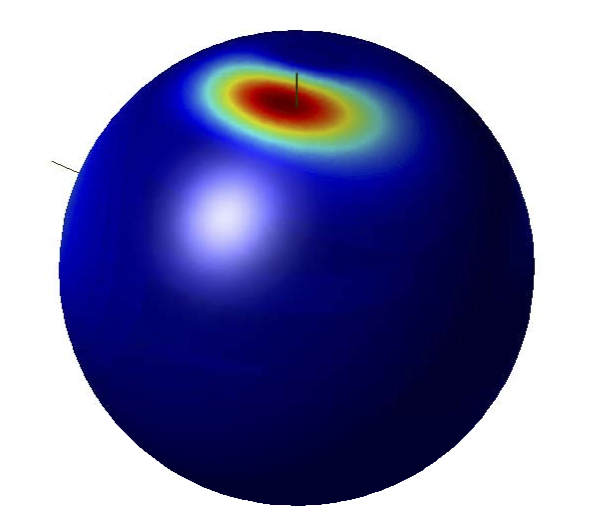

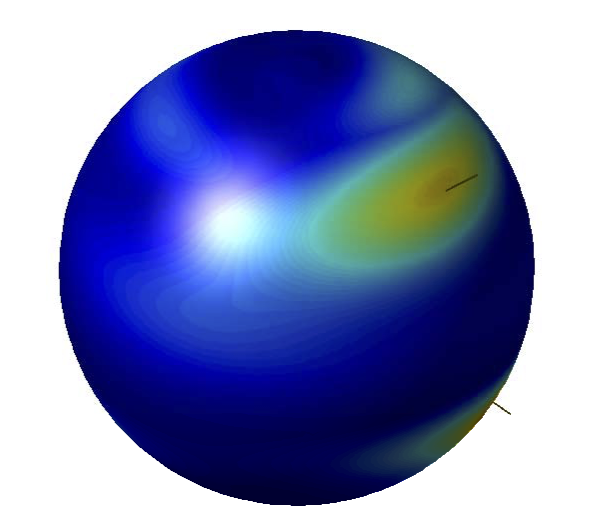
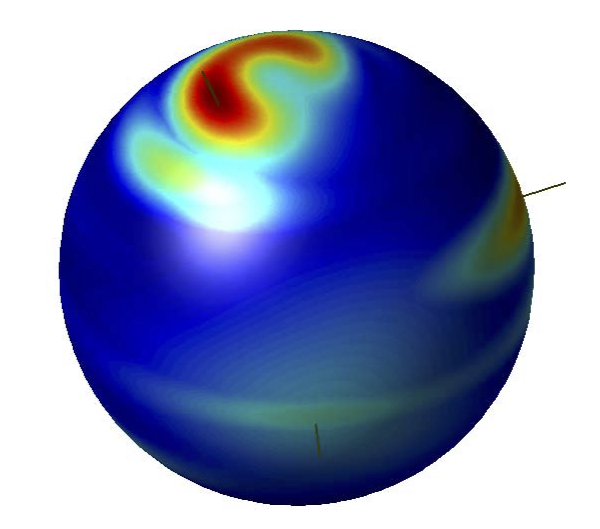
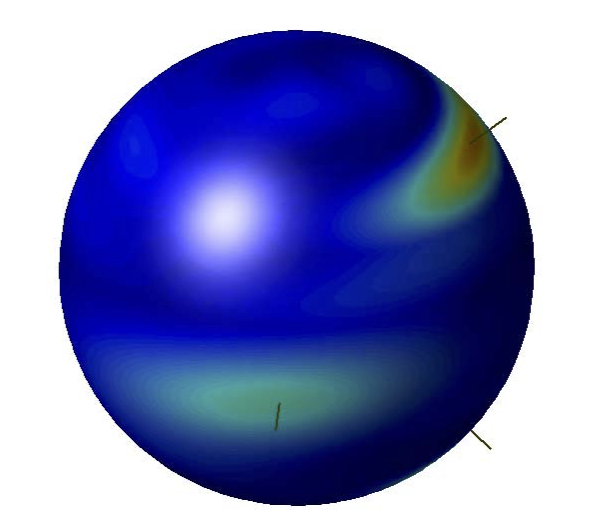
Figure: visualization of the propagated attitude probability density on the unit-sphere
Video: Spectral Uncertainty Propagation of Hybrid Systems - Bouncing Ball
Concurrent Bayesian Learning and Bayesian Estimation
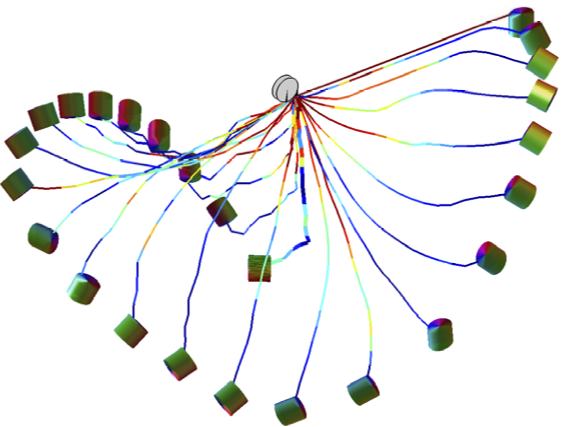
Despite numerous fascinating applications of model-free reinforcement learning, completely discarding the underlying dynamics might not be desirable in various control problems in aerial robotics, as by doing so, valuable information encoded in the dynamics will be lost. A more reasonable approach would be identifying the discrepancy between the pre-determined mathematical model and the actual response, or constructing a dynamic model completely from experiences.In such cases, it is critical to formulate a measure of confidence in the learned model such that the corresponding controller becomes aware of risky actions caused by large uncertainties in the learned model, or to avoid the model being constantly drifted by noisy measurements. Bayesian learning, often described as a neural network which is aware of what it does not know, will address such issue of learning with uncertainties. However, in learning a dynamic model, we often don’t have a direct access to the sample values of unknown terms. Instead, a subset of the state or a lower-dimensional function of state is measured by a sensor. For example, unmanned aerial vehicles are rarely equipped with a velocity sensor, and the velocity is estimated by measurements of position and acceleration.
As such, Bayesian learning should be integrated with Bayesian estimation for stochastic learning of dynamics. But most of learning-based control systems often assume that the state is available such that the uncertain term can be directly inferred. Concurrent stochastic learning and estimation is one of the main directions that I plan to pursue in the next five years. Figures below illustrate one preliminary result, where the uncertain part of the dynamics (red) is learned as a function of state with a Gaussian process (blue) that is extended to handles uncertainties in the input
Figure: Bayesian learning of state-dependent uncertainties